Por : Josué Zapeta
viernes, 21 de febrero de 2014
ELEMENTOS DE LÓGICA
PROPOSICIÓN
Tomada la “proposición”
como acepción lógica, podemos decir que es “la expresión de un juicio entre dos
términos”, que solo puede ser
“verdadera” o “falsa”, pero no puede ser verdadera y falsa a la vez o
simultáneamente.
Una expresión de la cual no
se puede decir si es verdadera o falsa, no es una proposición.
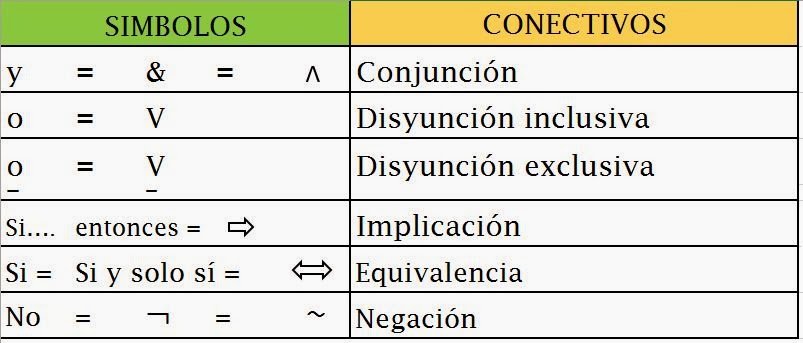
CONECTIVOS
Las proposiciones compuestas
requieren del uso de “conectivos”, o
sea que para relacionar las proposiciones simples se hace necesario la
aplicación de conectivos, y estos son:
Representación de las proposiciones
Estas se pueden representar
por medio de letras, o sea qué, a cada proposición se le debe asignar una letra
para no escribir toda la proposición, estas letras pueden ser: p, q, r, s, t,
etc.
Valores de verdad
Conviene señalar aquí que la
proposición sencilla o simple sólo puede tener dos valores de verdad, que sea “VERDADERA”
o bien, que sea “FALSA”
EJEMPLO:
·
3 + 5 = 8 ésta proposición es verdadera.
· 12 – 3 = 6 ésta proposición es falsa
O sea que una proposición
simple puede tener dos valores de verdad, que sea verdadera o que sea falsa,
pero nunca verdadera y falsa a la vez.
ü Pero
cuando se trata de una proposición compuesta de dos proposiciones simples, los
valores posibles son cuatro.
ü Cuando
se tiene una proposición compuesta de tres proposiciones simples, los valores
posibles son ocho, y
ü Cuando
una proposición compuesta de cuatro proposiciones simples, los casos posibles
son dieciséis.
De lo anterior se deduce que
para una proposición compuesta de “n” proposiciones simples existen 2n valores,
donde 2 es una constante y “n” es el número de proposiciones simples.
Por ejemplo:
En el caso de cinco
proposiciones simples se tendrán:
25 = 2 x 2 x 2 x
2 x 2 = 32 valores posibles
25 = 2 x 2 = 4 x 2 = 8 x 2 = 16 x 2 = 32
|
21
|
|
p
|
|
V
F
|
|
22
|
|
|
p
|
q
|
|
V
V
F
F
|
V
F
V
F
|
|
23
|
||
|
p
|
q
|
r
|
|
V
V
V
V
F
F
F
F
|
V
V
F
F
V
V
F
F
|
V
F
V
F
V
F
V
F
|
|
24
|
|||
|
p
|
q
|
r
|
s
|
|
V
V
V
V
V
V
V
V
F
F
F
F
F
F
F
F
|
V
V
V
V
F
F
F
F
V
V
V
V
F
F
F
F
|
V
V
F
F
V
V
F
F
V
V
F
F
V
V
F
F
|
V
F
V
F
V
F
V
F
V
F
V
F
V
F
V
F
|
NEGACIÓN
La negación (~) de
una proposición es falsa si la proposición es verdadera y si la proposición es
falsa, la negación es falsa.
Ejemplo:
Tabla de verdad.
|
p
|
~p
|
|
V
V
F
F
|
F
F
V
V
|
CONJUNCIÓN
La conjunción (۸) de dos proposiciones es verdadera sólo en
el caso en que ambas sean verdaderas, y falsas, si una de las partes o ambas
son falsas.
EJEMPLO:
|
p
|
q
|
p ۸ q
|
|
V
V
F
F
|
V
F
V
F
|
V
F
F
F
|
DISYUNCIÓN
La disyunción puede ser
inclusiva o exclusiva. Cuando se trata de la disyunción exclusiva se indica
colocando debajo del símbolo una rayita así o, V, o bien haciendo
la aclaración de alguna otra forma de lo contrario se trata de la disyunción
inclusiva.
DISYUNCIÓN INCLUSIVA
La disyunción inclusiva (V)
de dos proposiciones es verdadera, siempre que al menos una de las
proposiciones sea verdadera, o bien que, la disyunción sea verdadera cuando una
de sus partes o ambas sean verdaderas, y que sea falsa cuando ambas partes sean
falsas.
EJEMPLO:
|
p
|
q
|
p V q
|
|
V
V
F
F
|
V
F
V
F
|
V
V
V
F
|
DISYUNCIÓN EXCLUSIVA
La disyunción exclusiva (V)
es verdadera cuando sólo una de las partes es verdadera, y falsa, cuando ambas
componentes son verdaderas a ambas son falsas.
EJEMPLO:
|
p
|
q
|
p V q
|
|
V
V
F
F
|
V
F
V
F
|
F
V
V
F
|
IMPLICACIÓN
EJEMPLO:
|
p
|
q
|
→ p q
|
|
V
V
F
F
|
V
F
V
F
|
V
F
V
V
|
EQUIVALENCIA
EJEMPLO:
|
p
|
q
|
←→ p q
|
|
V
V
F
F
|
V
F
V
F
|
V
F
F
V
|